Wings (Flügel)
Inhaltsverzeichnis
XY-Wing (XY-Flügel)
Ein XY-Wing ist in Wirklichkeit eine kurze XY-Chain, die als Muster beschrieben wird und dadurch leichter gefunden werden kann. Man startet mit einer zweiwertigen Zelle (eine Zelle, die nur zwei Kandidaten enthält). Diese Zelle ist das Pivot (der Angelpunkt). Die möglichen Kandidaten im Pivot werden X und Y genannt. Nun versucht man, zwei andere Zellen zu finden, die das Pivot sehen können, die Pincer (Zangen). Eine dieser Zellen muss die Kandidaten X und Z enthalten (Z ist ein beliebiger Kandidat, der von X und Y verschieden ist) und die andere muss Y und Z enthalten. Z kann jetzt aus jeder Zelle eliminiert werden, die beide Pincer sieht.
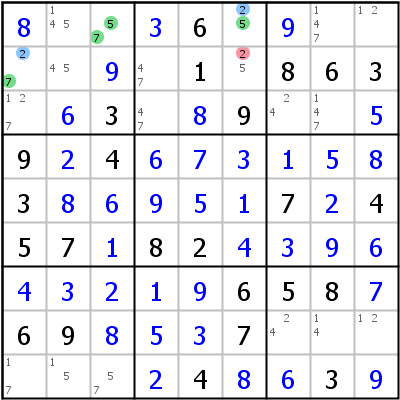
Linkes Beispiel: Zelle r1c3 (das Pivot) enthält Kandidaten 5 (X) und 7 (Y). Zelle r1c6 ist in der gleichen Zeile wie das Pivot und enthält Kandidaten 5 (X) und 2 (Z). Zelle r2c1 liegt im gleichen Block wie das Pivot und enthält Kandidaten 7 (Y) und 2 (Z). Zelle r2c6 sieht beide Pincer (r1c6 und r2c1). Sie kann nie 2 (Z) werden.
Die Logik ist einfach: Ist r1c3 5, muss r1c6 2 sein. Ist r1c3 7, muss r2c1 2 sein. In beiden Fällen kann r2c6 nicht 2 sein. Die äquivalente XY-Chain: 2- r2c1 -7- r1c3 -5- r1c6 -2 => r2c6<>2
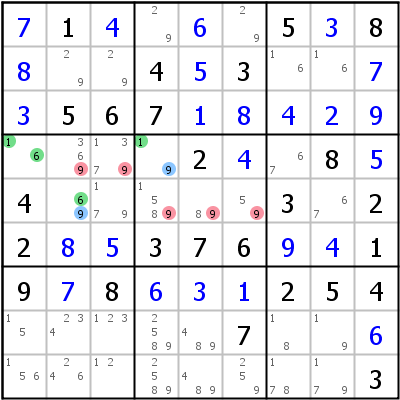
Rechtes Beispiel: X=1, Y=6, Z=9; Pivot in r4c1, Pincers in r4c4 und r5c2. Fünf Kandidaten können gelöscht werden.
XYZ-Wing (XYZ-Flügel)
Ein XYZ-Wing ist eine erweiterte Version des XY-Wings: Hier enthält das Pivot nicht nur die Kandidaten X und Y, sondern auch Z. Dadurch kann Z natürlich nur aus Zellen gelöscht werden, die nicht nur die Pincer, sondern auch das Pivot sehen.


Linkes Beispiel: Pivot r7c2, Pincers r2c2 und r7c1. Wenn r7c2=4, r2c2=7 => r9c2<>7; wenn r7c2=5, r7c1=7 => r9c2<>7; wenn r7c2=7 => r9c2<>7.
Rechtes Beispiel: 4/7/6 in r23c4,r3c7 => r3c56<>6
Erweiterte Flügel mit noch mehr Kandidaten sind zwar beschrieben worden, sie sind allerdings schwer zu finden und werden von HoDoKu nicht unterstützt.
W-Wing (W-Flügel)
W-Wings sind leicht zu finden und oft sehr effektiv. Sie bestehen aus zwei zweiwertigen Zellen mit denselben Kandidaten, die durch einen strong link für einen der beiden Kandidaten miteinander verbunden sind. Der andere Kandidat kann aus allen Zellen gelöscht werden, die beide zweiwertigen Zellen sehen können. Da ein W-Wing intern eine Chain ist, ist ein als Text niedergeschriebener Beweis wie unten zu sehen kompliziert. Das Muster selbst ist allerdings leicht zu finden (Filter können dabei eine große Hilfe sein).
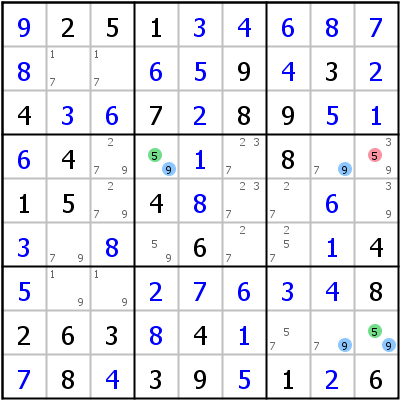
Linkes Beispiel: Die zweiwertigen Zellen sind r4c4 und r8c9 (Kandidaten 5 und 9). Der strong link existiert für Kandidat 9 in Spalte 8 (Spalte 8 hat nur zwei Möglichkeiten für Kandidat 9, was bedeutet, dass, wenn eine dieser Möglichkeiten nicht gesetzt ist, die andere gesetzt werden muss - strong link). Ein Ende des strong links sieht r4c4, das andere sieht r8c9. Kandidat 5 kann von allen Zellen gelöscht werden, die r4c4 und r8c9 sehen (im Beispiel ist das r4c9).
Beweis: Wir konzentrieren uns auf den strong link in Spalte 8: Einer der beiden Kandidaten 9 in r48c8 muss gesetzt sein. Ist r4c8=9, muss r4c4 5 sein. Ist r8c8=9, muss r8c9 5 sein. Eine der beiden Zellen r4c4 und r8c9 muss also in jedem Fall 5 sein, jede Zelle, die diese beiden Zellen sieht, kann nicht 5 sein.
Ein W-Wing ist natürlich eigentlich auch eine Chain. Das obige Beispiel als Discontinuous Nice Loop: r4c9 -5- r4c4 -9- r4c8 =9= r8c8 -9- r8c9 -5- r4c9.
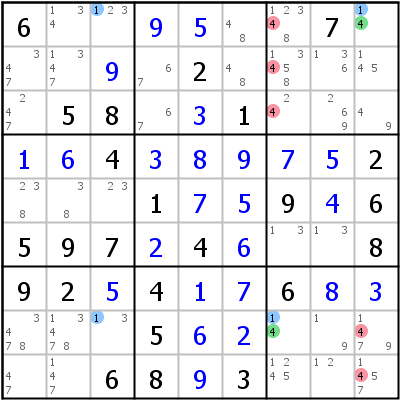
Rechtes Beispiel: W-Wing: 4/1 in r1c9,r8c7 verbunden durch 1 in r18c3 => r123c7,r89c9<>4
Copyright © 2008-12 by Bernhard Hobiger
Alles Material auf dieser Site unterliegt der GNU FDLv1.3.

