Naked Subsets (Nackte Untermengen)
Inhaltsverzeichnis
- Naked Pair/Locked Pair (Nacktes Paar/Gesperrtes Paar)
- Naked Triple/Locked Triple (Nackte Dreiergruppe/Gesperrte Dreiergruppe)
- Naked Quadruple (nackte Vierergruppe)
- Wie man sie findet
Naked Pair/Locked Pair (Nacktes Paar/Gesperrtes Paar)
Naked Subsets funktionieren ähnlich wie Hidden Subsets, es geht allerdings nicht um Kandidaten, die nur noch in bestimmten Zellen vorkommen (wie bei Hidden Subsets), sondern um Zellen, die nur noch eine bestimmte Anzahl an Kandidaten enthalten.
Naked Pair (Nacktes Paar)
Wenn man zwei Zellen im selben Haus finden kann, die beide nur noch die selben zwei Kandidaten übrig haben, kann man diese Kandidaten aus allen anderen Zellen des Hauses löschen.


Linkes Beispiel: Zellen r8c3 und r8c4 sind beide im selben Haus (Zeile 8) und haben beide nur noch Kandidaten 3 und 9 übrig. Es folgt sofort, dass eine dieser Zellen 3 und die andere 9 sein muss (welche welche ist, ist noch unbekannt). Wir können aber sicher sagen, dass r8c2 nicht 3 sein kann. Das Sudoku benötigt ab da nur noch Singles.
Das rechte Beispiel zeigt ein Naked Pair in einem Block: r4c5, r5c6 bilden ein Naked Pair in Block 5 und eliminieren damit Kandidaten 8 und 9 aus allen anderen Zellen dieses Blocks.
Locked Pair (Gesperrtes Paar)
Sind die beiden Zellen, die das Naked Pair bilden, nicht nur auf ein Haus, sondern auf zwei Häuser beschränkt (eine Zeile und ein Block oder eine Spalte und ein Block), werden sie manchmal als Locked Pair bezeichnet. Die Kandidaten können in beiden Häusern gelöscht werden.
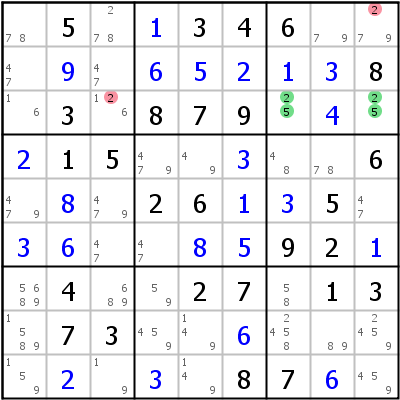

Im linken Beispiel bilden r3c79 ein Locked Pair in Zeile 3 und Block 3, 2 kann aus r3c3 (Zeile 3) und aus r1c9 (Block 3) gelöscht werden. Das rechte Beispiel zeigt ein Locked Pair in Zeile 8 und Block 8, 18 Kandidaten können gelöscht werden.
Naked Triple/Locked Triple (Nackte Dreiergruppe/Gesperrte Dreiergruppe)
Naked Triple (Nackte Dreiergruppe)
Kann man in einem Haus drei Zellen finden, die nur noch die selben Kandidaten übrig haben, kann man diese Kandidaten aus allen anderen Zellen dieses Hauses entfernen. Wichtig ist dabei, dass nicht alle Zellen alle Kandidaten enthalten müssen, aber in allen drei Zellen zusammen dürfen insgesamt nicht mehr als drei verschiedene Kandidaten sein.


Linkes Beispiel: Zellen r2c2, r4c2 und r5c2 sind alle im selben Haus (Spalte 2) und haben zusammen nur noch die Kandidaten 3, 6 und 9 übrig. Es folgt sofort, dass eine dieser Zellen 3, eine andere 6 und die letzte 9 sein muss (welche es konkret sind, ist noch unbekannt). Wir können aber sicher sein, dass r1c2 nicht 6 sein kann. Das Sudoku benötigt ab da nur noch Singles.
Das rechte Beispiel zeigt ein Naked Triple in einem Block: r3c45, r1c5 bilden ein Naked Triple in Block 2 und entfernen damit Kandidaten 1, 2 und 6 aus allen anderen Zellen in diesem Block.
Locked Triple (Gesperrte Dreiergruppe)
Wenn die drei Zellen, die das Naked Triple bilden, nicht nur auf ein Haus, sondern auf zwei Häuser beschränkt sind (eine Zeile und ein Block oder eine Spalte und ein Block), werden sie manchmal als Locked Triple bezeichnet. Kandidaten können aus beiden Häusern gelöscht werden.


Im linken Beispiel bilden r789c5 ein Locked Triple in Spalte 5 und Block 8, 9 kann aus r8c4 (Block 8) und aus r2c5 (Spalte 5) gelöscht werden. Das rechte Beispiel zeigt ein Locked Triple für 5, 6 und 7 in Zeile 5 und Block 6, das 18 Kandidaten eliminiert.
Naked Quadruple (Nackte Vierergruppe)
Naked Quadruples funktionieren gleich wie Naked Triples und Naked Pairs, nur werden jetzt vier Kandidaten in vier Zellen benötigt. Da eine Schnittmenge zwischen einer Zeile und einem Block oder zwischen einer Spalte und einem Block maximal drei Zellen haben kann, kann es kein Locked Quadruple geben.
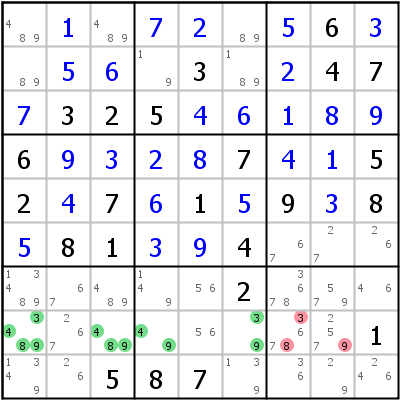

Das linke Beispiel zeigt ein Naked Quadruple in Zeile 8: Kandidaten 3, 4, 8 und 9 in Zellen r8c1346, gelöscht werden 3 und 8 von r8c7 und 9 von r8c8. Das rechte Beispiel hat das Naked Quadruple in Block 7: Kandidaten 4, 6, 7 und 9 in Zellen r8c2, r789c3.
Wie man sie findet
Am besten lassen sich Naked Subsets finden, wenn alle Markierungen eingetragen wurden. Ist das geschehen, kann man sie leicht erkennen, und sie sind auch normalerweise sehr effizient.
Copyright © 2008-12 by Bernhard Hobiger
Alles Material auf dieser Site unterliegt der GNU FDLv1.3.

