Single Digit Patterns (Einzelziffer-Muster)
Inhaltsverzeichnis
- Skyscraper (Wolkenkratzer)
- 2-String Kite (Papierdrache)
- Turbot Fish (Steinbutt)
- Empty Rectangle (Leeres Rechteck)
Skyscraper (Wolkenkratzer)
Ein Skyscraper ist ein einfaches Muster, das ziemlich häufig in Sudokus zu finden ist und das auch leicht gefunden werden kann. Es ist eigentlich nichts neues: Ein Skyscraper ist eine Sonderform eines Turbot Fish und kann als Kombination zweier Sashimi X-Wings aufgefasst werden.
Die Beschreibung des Musters klingt komplizierter als es eigentlich ist: Man konzentriert sich auf eine Ziffer. Nun versucht man zwei Zeilen (Spalten) zu finden, die nur noch je zwei Kandidaten für die Ziffer haben. Sind zwei dieser Kandidaten in derselben Spalte (Zeile), muss einer der beiden anderen wahr sein. Alle Kandidaten, die diese beiden Zellen sehen, können gelöscht werden.


Linkes Beispiel: In Spalte 6 kann Ziffer 1 nur noch in Zeile 1 oder Zeile 5 platziert werden. In Spalte 9 geht Ziffer 1 nur noch in Zeile 3 oder Zeile 5. r5c6 und r5c9 sind in derselben Zeile (das "Fundament" des Wolkenkratzers). Nun kann man sich folgendes überlegen: Wenn r1c6 nicht gesetzt ist, muss r5c6 gesetzt werden (nur zwei mögliche Positionen, eine davon muss gesetzt sein: strong link). Wenn aber r5c6 gesetzt ist, kann r5c9 nicht gesetzt sein, da beide Zellen in der selben Zeile sind (weak link). Und wenn schließlich r5c9 nicht gesetzt ist, muss r3c9 gesetzt sein (strong link). Wir haben eben bewiesen, dass r3c9 gesetzt sein muss, wenn r1c6 nicht gesetzt ist. Die gleiche Argumentation greift, wenn man mit "r3c9 nicht gesetzt" beginnt: r1c6 muss dann gesetzt sein. Da nun eine der beiden Zellen r1c6 und r3c9 gesetzt sein muss, können alle Kandidaten gelöscht werden, die beide Zellen sehen (im Beispiel: r1c78 und r3c45).
Glücklicherweise ist es nicht nötig, diese Übung in Logik jedes Mal durchzuführen, wenn man einen Skyscraper finden will. Es genügt natürlich, das Muster zu finden.
Die Stellen, an denen die Kandidaten des Skyscrapers liegen können, unterliegen einer Einschränkung: Die beiden oberen Zellen müssen im selben Band sein, sonst kann nichts eliminiert werden.
Das rechte Beispiel zeigt einen Skyscraper, der um 90 Grad im Uhrzeigersinn gedreht worden ist: Skyscraper für 4 in r2c5,r8c4 (verbunden durch r28c1) => r1c4<>4
Wenn wir noch einmal das linke Beispiel anschauen, können wir leicht die beiden Sashimi X-Wings finden, aus denen der Skyscraper besteht: Der erste ist c59/r35, Fin in r1c6, gelöscht wird 1 von r3c45. Der zweite ist c59/r15, Fin in r3c9, gelöscht wird 1 von r1c78.
2-String Kite (Papierdrache)
Standardmuster
Ein 2-String Kite ist eine besondere Form eines Turbot Fish, die in vielen Sudokus gefunden werden kann. Beschreibung: Wir konzentrieren uns wieder auf eine Ziffer. Wenn wir eine Zeile und eine Spalte finden können, die nur noch zwei Kandidaten der Ziffer enthalten (die Schnüre des Drachens), so dass ein Kandidat der Zeile und ein Kandidat der Spalte sich im selben Block befinden, dann kann der Kandidat, der die beiden anderen Enden der Schnüre sieht, gelöscht werden.
2-String Kites arbeiten ähnlich wie Skyscrapers: Eines der beiden Enden der Schnüre muss wahr sein.


Linkes Beispiel: Die Ziffer ist 5. Die erste Schnur ist in Spalte 7 (Kandidaten r29c7), die andere ist in Zeile 8 (Kandidaten r8c49). Die Enden r9c7 und r8c9 sind beide in Block 9. Wenn r2c7 nicht gesetzt ist, muss r9c7 gesetzt sein, r8c9 darf nicht und r8c4 muss gesetzt sein. Wenn r8c4 nicht gesetzt ist, muss gleichermaßen r2c7 gesetzt sein. Egal wie, Zelle r2c4, die sowohl r2c7 als auch r8c4 sieht, kann jedenfalls nicht 5 sein.
Rechtes Beispiel: Kandidat 9, Schnüre r6c16 und r47c2, verbunden in Block 4: r7c6 kann nicht 9 sein.
Dual 2-String Kite (Doppelter Papierdrache)
Manchmal können die beiden im Block verbundenen Kandidaten an vier verschiedenen Schnüren festgebunden werden, wodurch de facto zwei 2-String Kites entstehen, die gemeinsam zwei Kandidaten eliminieren. Diese beiden 2-String Kites können als ein einzelner Zug gesehen werden und werden dann Dual 2-String Kite genannt. HoDoKu unterstützt duale Formen nur optional (jede duale Form kann immer durch ihre zwei Grundformen nachgebildet werden).

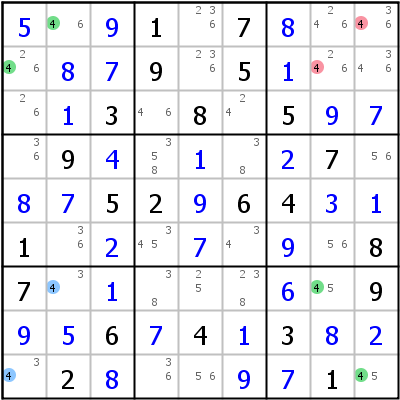
Linkes Beispiel: Die gemeinsamen Kandidaten sind r1c3 und r3c1 in Block 1. Die beiden Drachen, die mit ihnen gebildet werden können, sind: r1c38/r36c1 (r6c8<>1) und r3c19/r14c3 (r4c9<>1).
Rechtes Beispiel: Gemeinsame Kandidaten r7c2 und r9c1 in Block 7. Drachen: r29c1/r7c28 (r2c8<>4) und r17c2/r9c19 (r1c9<>4).
Turbot Fish (Steinbutt)
Ein Turbot Fish ist eigentlich eine Chain (Kette) und kein Fisch. Für eine detaillierte Beschreibung der verschiedenen Techniken und Ausdrücke für Chains siehe Chains: Einführung.
Ein Turbot Fish ist eine X-Chain, die genau vier Glieder lang ist. Verschiedene Muster können mit so einer Kette gebildet werden. Eines davon ähnelt einem Fisch, was der Strategie ihren Namen gab (rechtes Beispiel: Wenn man zwei Linien vom roten Kandidaten zum jeweils nächsten grünen und blauen Kandidaten zieht, kann man den Fisch erkennen).
Turbot Fishes sind etwas aus der Mode gekommen. Einer der Gründe liegt darin, dass die meisten grundlegenden Turbot-Muster als eigene Muster mit eigenen Namen beschrieben worden sind: Skyscraper, 2-String Kite und Empty Rectangle (letzteres nur mit nur zwei Kandidaten im leeren Rechteck selbst).


Die Beispiele zeigen zwei der Möglichkeiten als Turbot Fish: Links ein Empty Rectangle, rechts ein 2-String Kite.

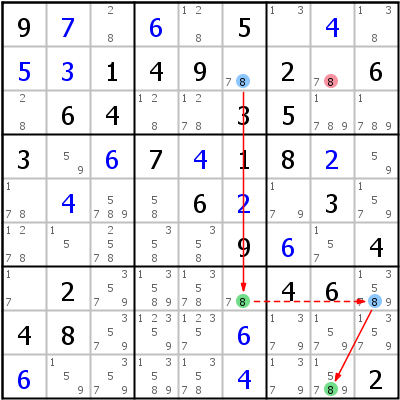
Die Beispiele: Links ein Skyscraper, rechts noch einmal ein Empty Rectangle (genauer: ein Dual Empty Rectangle).
Empty Rectangle (Leeres Rechteck)
Standardmuster
Empty Rectangles können auf verschiedene Art und Weise in sehr fortgeschrittenen Strategien verwendet werden. Das hier beschriebene Muster ist eine grundlegende Variante.
Zunächst definieren wir das Empty Rectangle (ER) selbst: Wenn ein Kandidat innerhalb eines Blocks nur noch in einer Zeile und einer Spalte vorkommt, formen die verbleibenden Zellen ein ER. Betrachten wir die Beispiele: Unten links ist Kandidat 9 in Block 5 auf Zeile 4 und Spalte 6 beschränkt. Das ER ist r5c45 und r6c45. Unten rechts ist Kandidat 1 in Block 5 auf Zeile 4 und Spalte 5 beschränkt. Das ER ist r5c46 und r6c46.
Wurde ein ER gefunden, kann es auf mögliche Eliminierungen geprüft werden: Man benötigt ein Conjugate Pair (eine Zeile oder Spalte, die nur noch zwei Kandidaten enthält), wobei einer dieser zwei Kandidaten in der Zeile (Spalte), die das ER bildet, liegt. Wenn die Spalte (Zeile) des ER einen Kandidaten enthält, der das andere Ende des Conjugate Pair sieht, kann er gelöscht werden.
Ein ER-Muster wie oben beschrieben kann immer auch als Finned Mutant X-Wing oder als Grouped Nice Loop gesehen werden.


Linkes Beispiel: Zeile 4 und Spalte 6 bilden ein ER in Block 5. Zellen r48c2 sind ein Conjugate Pair. Eine Seite des Conjugate Pairs ist in der ER-Zeile (r4c2), das andere Ende sieht einen Kandidaten in der ER-Spalte (r8c6). 9 kann aus r8c6 gelöscht werden.
Um zu sehen, warum das funktioniert, startet man am besten mit Kandidat 9 in r8c2. Wenn r8c2 9 ist, kann r8c6 nicht 9 sein (selbe Zeile). Wenn r8c2 nicht 9 ist, muss r4c2 9 sein (Conjugate Pair/Strong Link). Das bedeutet, dass weder r4c5 noch r4c6 9 sein kann. Dies wiederum lässt r6c6 als letzten Kandidaten in Block 5, er muss gesetzt werden und r8c6 kann wieder nicht gesetzt sein. Da beide Möglichkeiten in r8c2 zum selben Ergebnis führen (r8c6<>9), kann 9 von r8c6 gelöscht werden.
Der äquivalente Finned Mutant X-Wing: 9 c2b5 r4c6 fr8c2 => r8c6<>9.
Die äquivalente Grouped Nice Loop: r8c6 -9- r8c2 =9= r4c2 -9- r4c56 =9= r6c6 -9- r8c6 => r8c6<>9.
Im rechten Beispiel formen Zeile 4 und Spalte 5 das ER, r7c59 ist das Conjugate Pair und r4c9 kann eliminiert werden.
ERs mit nur zwei Kandidaten
Wenn im Block, der das ER enthält, nur noch zwei Kandidaten übrig sind, ist das Empty Rectangle nicht eindeutig bestimmt. Die Eliminierungen sind natürlich trotzdem gültig. Der Spielzug kann als Turbot Fish oder als X-Chain ausgeführt werden. Einige Sudoku-Spieler denken, dass ERs mit nur zwei Kandidaten nicht gültig sind, HoDoKu unterstützt sie daher nur optional.
Bitte beachten: Da Turbot Fisch in der Standard-Reihenfolge des Solvers vor ER kommt, werden ERs mit zwei Kandidaten immer als Turbot Fische gefunden, auch wenn die Option eingeschaltet ist. Um die unten gezeigten ERs als ERs zu finden, muss Turbot Fish hinter ER geschoben werden.


Linkes Beispiel: Empty Rectangle: 6 in b8 (r69c1) => r6c4<>6
Rechtes Beispiel: Empty Rectangle: 5 in b3 (r8c49) => r2c4<>5
Dual Empty Rectangle (Doppeltes Leeres Rechteck)
Manchmal formen der eliminierte Kandidat und das Ende des Conjugate Pairs ein eigenes Conjugate Pair. Wenn das der Fall ist, können beide Strong Links abwechselnd die Rolle des "Conjugate Pairs" übernehmen, was zu zwei verschiedenen Eliminierungen führt. Das Resultat wird Dual Empty Rectangle genannt.
Dual Empty Rectangles werden in HoDoKu optional unterstützt.
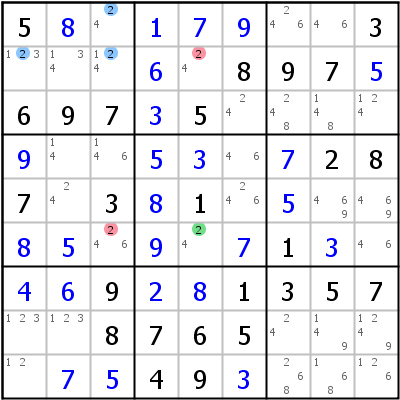
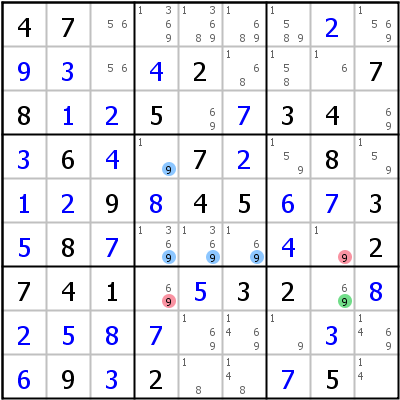
Im linken Beispiel wird das ER von Zeile 2 und Spalte 3 gebildet. r6c35 ist das Conjugate Pair, das 2 von r2c5 eliminiert. Da jedoch r26c5 ebenfalls ein Conjugate Pair ist, wird auch 2 aus r6c3 gelöscht.
Rechtes Beispiel: Dual Empty Rectangle: 9 in b5 (r67c8/r7c48) => r6c8,r7c4<>9
Copyright © 2008-12 by Bernhard Hobiger
Alles Material auf dieser Site unterliegt der GNU FDLv1.3.

