Uniqueness (Eindeutigkeit)
Inhaltsverzeichnis
- Einführung
- Unique Rectangle Type 1 (Ausschlussrechteck Typ 1)
- Unique Rectangle Type 2 (Ausschlussrechteck Typ 2)
- Unique Rectangle Type 3 (Ausschlussrechteck Typ 3)
- Unique Rectangle Type 4 (Ausschlussrechteck Typ 4)
- Unique Rectangle Type 5 (Ausschlussrechteck Typ 5)
- Unique Rectangle Type 6 (Ausschlussrechteck Typ 6)
- Hidden Rectangle (Verstecktes Rechteck)
- Avoidable Rectangle (Vermeidbares Rechteck)
- BUG+1 - Binary Universal Grave + 1 (Zweiwertiges Zifferngrab + 1)
- Unique Rectangles mit fehlenden Kandidaten
Einführung
Eindeutigkeit in Sudoku
Uniqueness Techniques (Eindeutigkeits-Strategien) basieren auf der Tatsache, dass praktisch jedes jemals publizierte Sudoku lediglich eine einzige gültige Lösung besitzt. Mehr noch: Die meisten Sudoku-Spieler sind der Meinung, dass Sudokus mit mehr als einer Lösung ungültig sind. Das bedeutet aber, dass jede Konstellation, die zu zwei oder mehr Lösungen führen könnte, die alle die Sudoku-Regel nicht verletzen, vermieden werden muss. Das Problem dabei ist, dass Eindeutigkeit von Sudokus nicht Teil der Sudoku-Regel ist ("jede Zeile, jede Spalte und jeder Block muss die Ziffern 1 bis 9 enthalten"). Das hat zu einer sehr hitzigen Diskussion darüber geführt, ob Uniqueness Strategien erlaubt sind oder nicht (siehe Uniqueness Controversy auf Sudopedia).
Ob man nun Uniqueness Strategien einsetzt oder nicht, ist zur Gänze eine Frage des persönlichen Geschmacks. Wenn man Sudokus löst, die in Büchern oder Zeitungen veröffentlicht wurden, kann man hinreichend sicher sein, dass sie nur eine eindeutige Lösung besitzen (für einige Ausnahmen siehe Hall of Shame). Wenn man ein Computerprogramm wie HoDoKu verwendet, wird die Anzahl der Lösungen bei der Eingabe automatisch geprüft, und das Programm gibt eine Warnung aus, wenn man versucht ein ungültiges Sudoku zu lösen (siehe auch das Benutzerhandbuch).
Uniqueness Strategien sind einfach zu finden, vielseitig und können oft Sudokus lösen, die sonst sehr komplizierte Strategien benötigen würden. HoDoKu hat daher Unterstützung für eine Vielzahl an Strategien eingebaut. Will man sie nicht verwenden (trotz ihrer offensichtlichen Vorteile), kann man alle Uniqueness Strategien mit einem einzigen Mausklick ausschalten ("Bearbeiten|Einstellungen", auf die Baumansicht umschalten).
Unique Rectangle (Ausschlussrechteck)
Ein Unique Rectangle (UR) besteht aus vier Zellen, die genau zwei Zeilen, zwei Spalten und zwei Blöcke belegen. Alle vier Zellen haben dieselben zwei Kandidaten übrig.

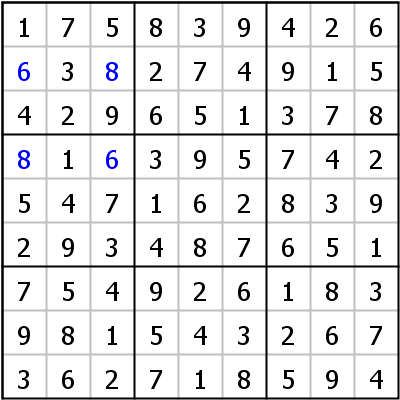
Das linke Beispiel ist dem Artikel Unique Rectangle der Sudopedia entnommen. Die Zellen r2c13 und r4c13 erfüllen alle nötigen Anforderungen. Zwei Zeilen (Zeilen 2 und 4), zwei Spalten (Spalten 1 und 3), zwei Blöcke (Blöcke 1 und 4) und zwei Kandidaten (Kandidaten 6 und 8).
Eine Situation wie oben beschrieben ist ungültig, weil die Kandidaten in den Zellen vertauscht werden können und so zwei verschiedene Lösungen erzeugen, die beide die Sudoku-Regel nicht verletzen (siehe unten). Wenn das Sudoku nur eine Lösung hat, muss jede Situation, die zu einem Unique Rectangle führen könnte, vermieden werden.
Die zwei (gültigen) Lösungen für das obige UR:

Ein beliebter Fehler beim Suchen von URs besteht darin, die "zwei Blöcke"-Regel zu verletzen (siehe Sudopedia Artikel für ein Beispiel).
Binary Universal Grave (BUG) (Zweiwertiges Zifferngrab)
Ein Binary Universal Grave (BUG) ist eine Verallgemeinerung eines UR: Ein BUG existiert, wenn alle noch ungelösten Zellen genau zwei Kandidaten haben und wenn jeder Kandidat in jeder Zeile, jeder Spalte und jedem Block genau zwei Mal vorkommt. Auch ein solches Sudoku hat zwei gültige Lösungen.
Unique Rectangle Type 1 (Ausschlussrechteck Typ 1)
Ein UR Typ 1 existiert, wenn genau eine Zelle eines möglichen URs zusätzliche Kandidaten hat. Würden diese Kandidaten gelöscht, würde das UR existieren und zwei Lösungen bewirken. Es ist daher absolut notwendig einen der zusätzlichen Kandidaten zu setzen. Das bedeutet, dass die UR-Kandidaten aus dieser Zelle gelöscht werden können. Wenn es nur einen zusätzlichen Kandidaten gibt, kann er sofort in der Zelle platziert werden.
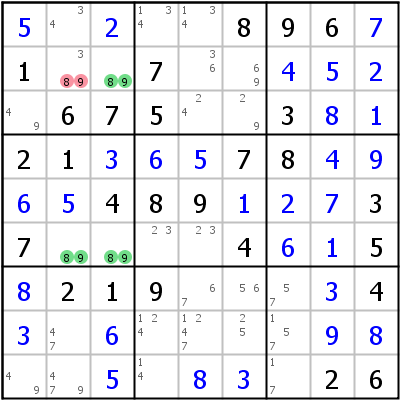
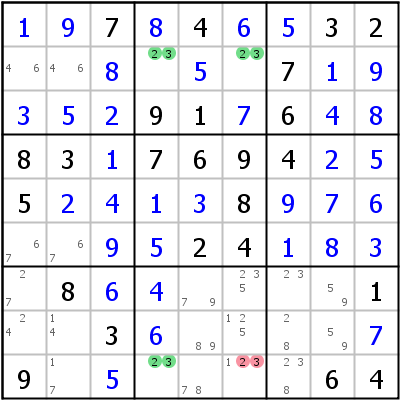
Im linken Beispiel bilden die Kandidaten 8 und 9 beinahe ein UR in r2c23 und r6c23. Das UR wird nur durch den zusätzlichen Kandidaten 3 in r2c2 verhindert. 8 und 9 können aus r2c2 eliminiert werden (oder 3 kann in r2c2 platziert werden).
Rechtes Beispiel: 2/3 in r2c46,r9c46 => r9c6<>23 (oder r9c6=1).
Unique Rectangle Type 2 (Ausschlussrechteck Typ 2)
Wenn in einem möglichen UR zwei nicht diagonale Zellen genau den gleichen zusätzlichen Kandidaten haben, können alle Kandidaten, die beide Extra-Kandidaten sehen, eliminiert werden.
Die Logik ist einfach: Um das UR zu vermeiden muss einer der beiden zusätzlichen Kandidaten gesetzt werden, daher kann der Kandidat in keiner Zelle gesetzt sein, die beide diese Zellen sieht.
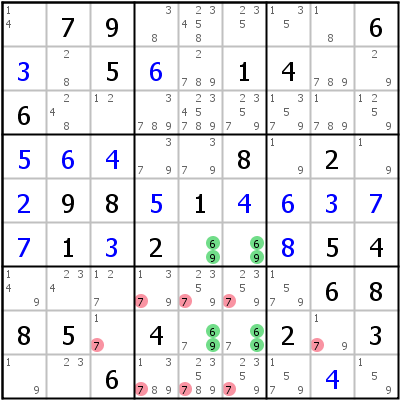
Linkes Beispiel: Wir haben ein mögliches UR für 3 und 7 in r7c29 und r8c29. Die beiden nicht diagonalen Zellen r78c9 haben einen Zusatzkandidaten 8. Eine dieser beiden Zellen muss 8 sein, sonst hätte das Sudoku zwei Lösungen. 8 kann daher auf keinen Fall in r9c9 gesetzt werden.
Ein UR Type 2 kann Kandidaten in mehr als einem Haus eliminieren, wie das rechte Beispiel zeigt: Die zusätzlichen 7er in r8c56 eliminieren alle anderen 7er sowohl in Zeile 8 als auch in Block 8.
Unique Rectangle Type 3 (Ausschlussrechteck Typ 3)
Diese Strategie kombiniert ein UR mit einem Naked/Locked Subset. Man sucht zwei nicht diagonale Zellen mit Zusatzkandidaten in einem möglichen UR. Da einer dieser Kandidaten gesetzt sein muss um das UR zu vermeiden, können beide Zellen als eine virtuelle Zelle aufgefasst werden, die nur die Zusatzkandidaten enthält. Mit dieser virtuellen Zelle kann man jetzt versuchen, ein Naked Subset zu bilden (alle zusätzlichen Zellen müssen natürlich beide UR-Zellen sehen können). Wenn so eine UR/Naked Subset-Kombination gefunden werden kann, können alle Subset-Kandidaten in allen Zellen außerhalb des Subsets (aber natürlich im selben Haus) eliminiert werden.


Linkes Beispiel: Mögliches UR für 1/5 in r4c28 und r6c28. Zelle r6c8 hat zwei zusätzliche Kandidaten 6 und 9 und Zelle r4c8 hat zwei zusätzliche Kandidaten 4 und 6. Wenn wir Zellen r46c8 als eine Zelle auffassen, die nur die Kandidaten 4, 6 und 9 enthält, können wir ein Naked Triple für diese drei Kandidaten in den Zellen r1c8, r2c8 und r46c8 bilden. Da die drei Kandidaten auf diese vier Zellen beschränkt sind, können sie weder in r8c8 noch in r9c8 gesetzt werden.
Das rechte Beispiel zeigt ein UR Type 3 mit einem Locked Pair: Die zusätzlichen Kandidaten 1 und 3 in r6c23 bilden das Locked Pair mit r6c1 (eingeschlossen in Zeile 6 und Block 4).
Unique Rectangle Type 4 (Ausschlussrechteck Typ 4)
Man sucht wieder nach Zusatzkandidaten in zwei nicht diagonalen Zellen, aber dieses Mal werden die Zusatzkandidaten ignoriert, man konzentriert sich auf die UR-Kandidaten: Wenn einer der UR-Kandidaten in dem Haus, das die beiden Extra-Zellen enthält, nirgendwo sonst mehr vorkommen kann, kann der andere UR-Kandidat aus diesen Zellen eliminiert werden.

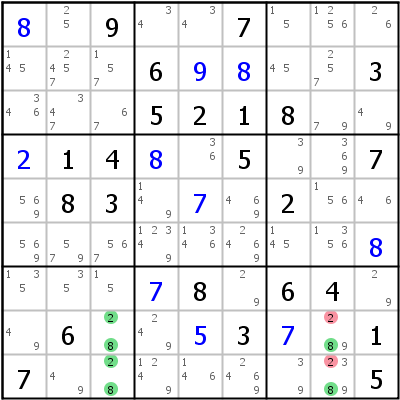
Um zu sehen, wie das funktioniert, betrachten wir das linke Beispiel: Mögliches UR für 6/7 in r3c79 und r6c79. r3c7 und r3c9 haben Zusatzkandidaten (das heißt: das sind die einzigen Zellen des URs, die überhaupt weder 6 noch 7 sein können). Es gibt zwei Häuser, die sowohl die Zelle r3c7 als auch die Zelle r3c9 sehen können; Zeile 3 und Block 3. Zeile 3 hat den Kandidaten 6 nur in den UR-Zellen (das gilt auch für Block 3, aber das ist nicht nötig - ein Haus reicht völlig), also muss 6 entweder in r3c7 oder in r3c9 gesetzt werden. Das aber heißt, dass 7 weder in r3c7 noch in r3c9 gesetzt sein darf, sonst hätten wir ja ein UR. Wir können also 7 aus r3c79 eliminieren.
Die gleiche Logik gilt für das rechte Beispiel: UR-Kandidat 8 ist nirgendwo sonst in Spalte 8 (oder Block 9) möglich, also kann 2 eliminiert werden. Man sollte beachten, dass zusätzliche Kandidaten 8 in einem der beiden Häuser (Spalte 8 oder Block 8) vorhanden sein dürften, allerdings nicht in beiden. So eine Situation ist aber nicht sehr wahrscheinlich, weil die zusätzlichen 8er normalerweise vorher mit einem Locked Candidates-Zug eliminiert worden wären.
Unique Rectangle Type 5 (Ausschlussrechteck Typ 5)
UR Typ 5 ist eine Variante von UR Typ 2, hier kann der Zusatzkandidat allerdings auch in diagonalen Zellen sein. Nehmen wir an, wir hätten ein mögliches UR mit einem Zusatzkandidaten in entweder zwei diagonalen oder aber in drei Zellen des URs. Der Zusatzkandidat kann aus allen Zellen gelöscht werden, die alle UR-Zellen mit diesem Kandidaten sehen können. Die Logik hinter dieser Strategie ist ganz gleich wie beim UR Type 2.

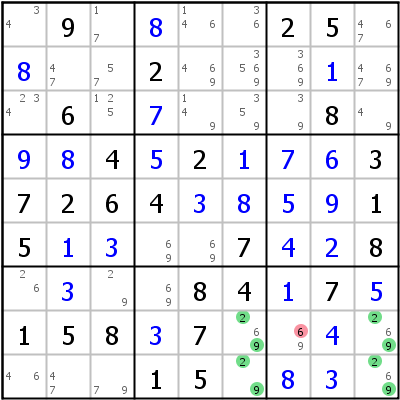
Das linke Beispiel ist das einzige derzeit veröffentlichte Beispiel für ein UR Typ 5 mit nur zwei Zusatzkandidaten: 1 muss entweder in r7c8 oder in r8c5 gesetzt sein um das UR zu vermeiden. Zelle r7c4 sieht diese beiden UR-Zellen und kann daher selber nicht 1 sein.
Das UR Type 5 im rechten Beispiel hat drei Zusatzkandidaten: 6 muss in r8c6, r8c9 oder r9c9 sein. Es kann aus r8c7 gelöscht werden.
Unique Rectangle Type 6 (Ausschlussrechteck Typ 6)
UR Typ 6 ist eine Variante von UR Typ 4. Es ist nicht sehr häufig, aber sehr effektiv, weil es immer zu zwei Platzierungen führt: Angenommen es existiert ein mögliches UR mit zwei diagonalen Zellen mit Zusatzkandidaten. Wenn einer der UR-Kandidaten in den beiden Zeilen und Spalten, die das UR bilden, nirgendwo außerhalb des URs vorkommen kann, kann er aus den Zellen mit den Zusatzkandidaten gelöscht werden.


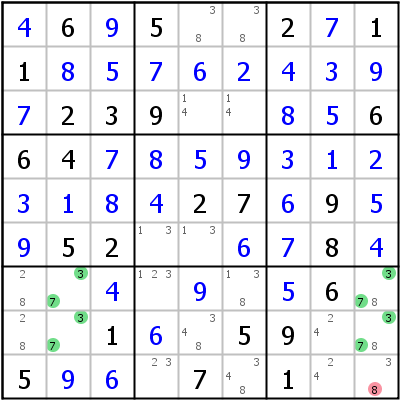
Linkes Beispiel: In Zeilen 4 und 5 und Spalten 3 und 4 existiert Kandidat 5 nur mehr im UR: Er bildet einen X-Wing. Würde 5 in einer der Zellen r4c3/r5c4, die die Zusatzkandidaten enthalten, gesetzt, müsste 5 in der anderen Zelle ebenfalls gesetzt werden, was ein UR und damit zwei Lösungen erzwingen würde. Man kann daher sicher sein, dass 5 in keiner dieser Zellen vorkommen kann.
Das rechte Beispiel zeigt ein UR Typ 6 für Kandidat 7. Übrigens existiert für jedes UR Typ 6 ein Paar von Hidden Rectangles, die beide zu den gleichen Platzierungen führen.
Hidden Rectangle (Verstecktes Rechteck)
Hidden Rectangles sind sehr vielseitig, weil sie in möglichen URs eingesetzt werden können, die bis zu drei Zellen mit beliebigen Zusatzkandidaten enthalten (das UR ist unter einem Haufen von Zusatzkandidaten versteckt - nicht zu verwechseln mit einem Almost Unique Rectangle).
Man benötigt ein mögliches UR mit zwei oder drei Zellen mit Zusatzkandidaten (gibt es nur eine solche Zelle, sollte das UR Typ 1 verwendet werden). Nun nimmt man eine UR-Zelle ohne Zusatzkandidat als Ausgangspunkt und prüft die Zeile und die Spalte, die die schräg gegenüberliegende Ecke des URs enthalten. Darf einer der UR-Kandidaten in diesen beiden Häusern nirgendwo außerhalb des URs vorkommen, kann der andere UR-Kandidat aus der gegenüberliegenden Ecke gelöscht werden.
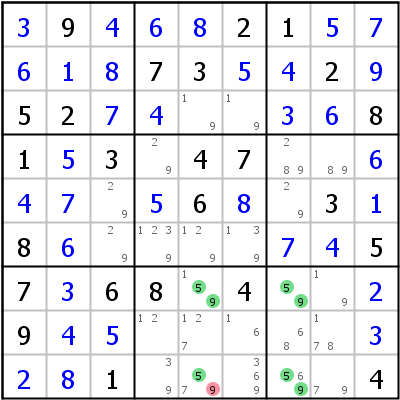

Um zu sehen, warum das funktioniert, betrachten wir das linke Beispiel: Es gibt nur eine Zelle ohne Zusatzkandidaten: r7c7. Diese Zelle wird unser Ausgangspunkt. Die schräg gegenüberliegende Ecke ist Zelle r9c5, die in Zeile 9 und Spalte 5 enthalten ist. Kandidat 5 kommt außerhalb des URs in diesen beiden Häusern nicht mehr vor, also kann 9 aus r9c5 gelöscht werden. Warum? Wenn wir Spalte 5 betrachten, sehen wir, dass Kandidat 5 entweder in r7c5 oder in r9c5 gesetzt werden muss. Wenn 5 in r9c5 gesetzt wird, kann diese Zelle natürlich nicht 9 sein. Wird 5 in r7c5 gesetzt, kann 5 nicht in r9c5 sein, 5 muss also in r9c7 gesetzt werden. Das zwingt r7c7 auf 9 und das wiederum bedeutet, dass r9c5 nicht auch 9 sein kann, sonst hätten wir wieder zwei Lösungen. Da beide möglichen Platzierungen des Kandidaten 5 in Spalte 5 zu r9c7<>9 führen, kann 9 aus dieser Zelle gelöscht werden.
Das rechte Beispiel hat nur zwei Zellen mit zusätzlichen Kandidaten, was bedeutet, dass zwei mögliche Ausgangspunkte geprüft werden müssen: r2c9 und r3c2. Versuchen wir zuerst r2c9: Die gegenüberliegende Ecke ist in Zeile 3 und Spalte 2. Wir sehen nun, dass Zeile 3 eine 4 und eine 5 außerhalb des URs hat, es ist also kein Hidden Rectangle möglich.
Jetzt r3c2: Die Häuser, die geprüft werden müssen, sind Zeile 2 und Spalte 9. Kandidat 4 gibt es nirgendwo mehr in diesen Häusern (außer im UR natürlich), also kann 5 aus r2c9 gelöscht werden.
Avoidable Rectangle (Vermeidbares Rechteck)
Ein Avoidable Rectangle unterscheidet sich von einem Unique Rectangle dadurch, dass einige Zellen des UR bereits gesetzt worden sind. Wenn das Setzen der restlichen Zellen ein UR bewirkt, dann hätte der Erzeuger des Sudokus eine der vier Zellen als Angabe setzen müssen um eine mögliche zweite Lösung zu vermeiden (daher der Name). Wenn also keine der bereits gesetzten Zellen Teil der Angabe ist, können alle UR Type x-Regeln ohne Änderungen angewendet werden.
Einen wichtigen Unterschied gibt es allerdings: Durch die bereits erfolgten Platzierungen kann es vorkommen, dass nur mehr einer der UR-Kandidaten in der Zielzelle übrig ist. Das kann zwar verwirrend sein, aber die Logik der Strategien wird davon nicht beeinflusst.
HoDoKu unterstützt derzeit nur Avoidable Rectangles Type 1 und 2.
Avoidable Rectangle Type 1 (Vermeidbares Rechteck Typ 1)
Analog zu Unique Rectangle Type 1.

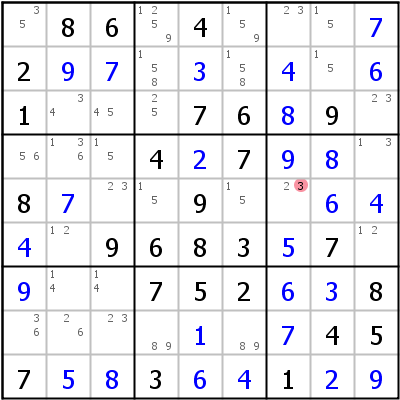
Linkes Beispiel: Das mögliche UR ist für Kandidaten 7 und 9 in Zellen r12c19. Die einzige noch nicht gesetzte Zelle ist r2c9, alle anderen Zellen gehören nicht zur Angabe. Wenn 9 in r2c9 gesetzt würde, könnten die Ziffern 7 und 9 in den vier UR-Zellen ausgetauscht werden, was zwei Lösungen bewirken würde. Da das nicht möglich ist, kann r2c9 nicht 9 sein.
Wichtig ist, dass die Logik nur angewendet werden kann, wenn keine der Zellen zur Angabe gehört. Ist auch nur eine der Zellen in der Angabe enthalten, können die Ziffern nicht mehr vertauscht werden und es gibt immer noch nur eine Lösung für das Sudoku.
Rechtes Beispiel: Avoidable Rectangle Type 1: 6/3 in r57c78 => r5c7<>3
Avoidable Rectangle Type 2 (Vermeidbares Rechteck Typ 2)
Analog zu Unique Rectangle Type 2. Type 2 läßt sich leichter erkennen, weil beide UR-Kandidaten noch als Kandidaten sichtbar sind.
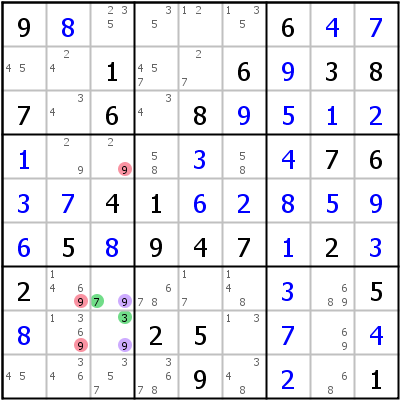

Linkes Beispiel: UR für Kandidaten 3 und 7 in r78c37, weder r7c7 noch r8c7 gehören zur Angabe. Zusätzlicher Kandidat 9 in r78c3, 9 kann von allen Zellen gelöscht werden, die diese beiden Zellen sehen.
Rechtes Beispiel: Avoidable Rectangle Type 2: 2/8 in r45c37 => r18c7,r456c9,r56c8<>9
BUG+1 - Binary Universal Grave + 1 (Zweiwertiges Zifferngrab + 1)
Ein BUG+1 ist ein möglicher BUG, bei dem genau eine Zelle genau einen zusätzlichen Kandidaten hat. Dieser Kandidat muss platziert werden um den BUG zu vermeiden.
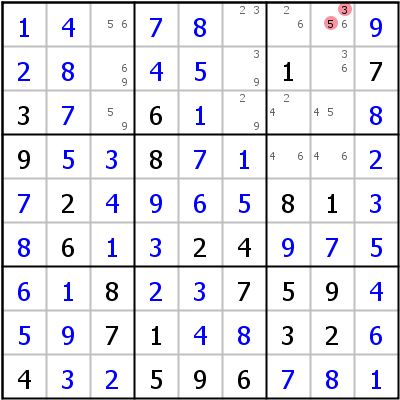
Linkes Beispiel: Der Zusatzkandidat ist Kandidat 6 in r1c8 (kommt öfter als zwei Mal in mindestens einem Haus vor). Er kann gesetzt werden (oder 3 und 5 können gelöscht werden).
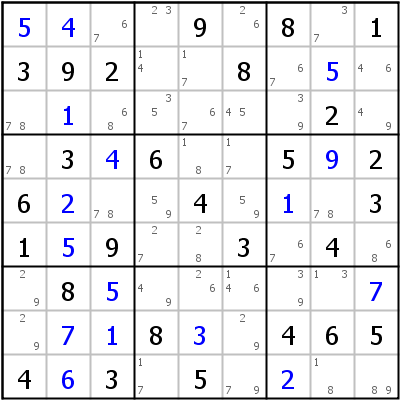
Rechtes Beispiel: Dies ist kein BUG+1! Wir haben zwar nur Zellen mit zwei Kandidaten übrig (Ausnahme: r7c6), aber die Bedingung für einen BUG ist nicht erfüllt: In Zeile 7 kommt Kandidat 9 drei mal vor (r7c147). Das Gleiche gilt für Spalte 6.
Unique Rectangles mit fehlenden Kandidaten
Damit ein Unique Rectangle funktionieren kann, müssen nicht unbedingt alle UR-Kandidaten in allen UR-Zellen vorhanden sein. Die einzige wirklich notwendige Bedingung ist, dass jede UR-Zelle alle UR-Kandidaten enthalten hätte können (das bedeutet: kein UR-Kandidat darf in einer UR-Zelle durch eine Zahl der Angabe blockiert sein). Das kann wichtig werden, wenn UR-Kandidaten bereits durch einen früheren Lösungsschritt eliminiert worden sind, was natürlich das UR ungültig machen würde, gälte oben Gesagtes nicht.
HoDoKu erlaubt fehlende Kandidaten in URs, wenn die Option "Fehlende Kandidaten in URs" in "Einstellungen|Lösungsschritte" gesetzt ist (siehe Optionen für Lösungstechniken im Benutzerhandbuch).
Einige Beispiele:


Linke Seite: UR Typ 1; r3c4 enthält den UR-Kandidaten 2 nicht mehr, aber 2 ist auch nicht durch die Angabe blockiert, daher ist das UR Typ 1 trotzdem gültig. Rechte Seite: UR Typ 2; UR-Kandidat 5 fehlt von r3c8.

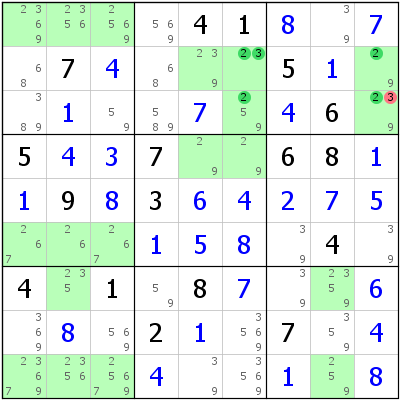
Linke Seite: UR Typ 6, UR-Kandidat 8 fehlt in r3c9 und r6c7; die Eliminierungen sind trotzdem gültig. Rechte Seite: Hidden Rectangle, Kandidat 3 fehlt in r2c9 und r3c6.
Copyright © 2008-12 by Bernhard Hobiger
Alles Material auf dieser Site unterliegt der GNU FDLv1.3.

