Intersections
Table of Contents
Locked Candidates Type 1 (Pointing)
If in a block all candidates of a certain digit are confined to a row or column, that digit cannot appear outside of that block in that row or column.


Look at the left example: In block 1 candidate 5 can only go into row 3. That means, that one of the cells r3c1 or r3c2 has to be 5, or block 1 would be without 5, which is not possible. It also means, that 5 can be eliminated from r3c7, because r3c7 sees both r3c1 and r3c2. The sudoku solves with singles after that move.
Locked candidates moves can eliminate up to 6 candidates as can be seen in the example on the right: In box 8 candidate 1 is locked in row 7 and can therefore be eliminated from the intersection of boxes 7 and 9 with row 7.
Locked Candidates Type 2 (Claiming)
Locked Candidates Type 2 works exactly the other way round: If in a row (or column) all candidates of a certain digit are confined to one block, that candidate that be eliminated from all other cells in that block.

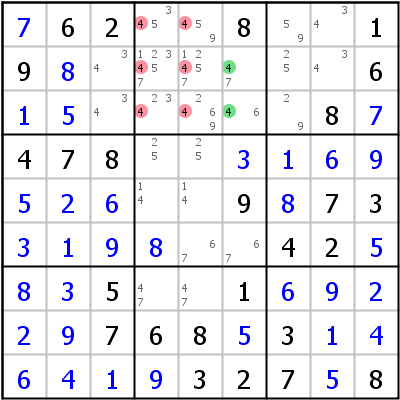
Look at the left example: In row 2 candidate 7 can only go into block 1. It can be eliminated from all cells in block 1 that don't belong to row 2, in our case cell r3c2. The sudoku solves with singles afterwards.
The example on the right shows a Locked Candidates move in a column: All 4s in column 6 are in block 2. They can be eliminated anywhere else in that block as shown in the image.
How to find them
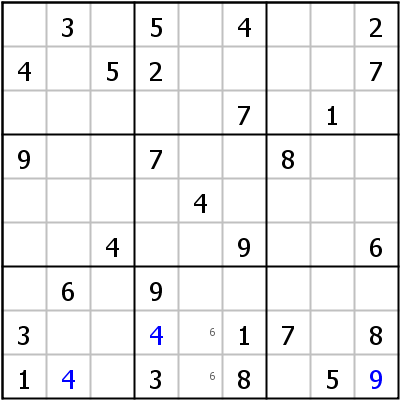
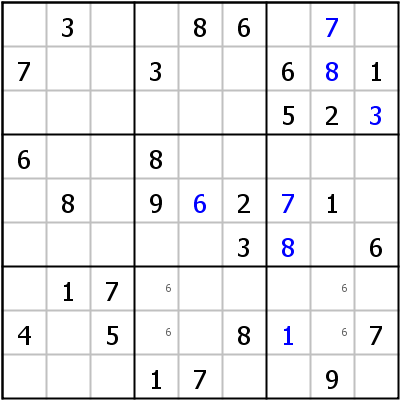
Locked Candidates moves are usually found by inserting pencil marks into the grid whenever a candidate is confined to one row or column within a block. Look at the example on the left side: The 6 in r7c2 blocks row 7. In block 8 candidate 6 can therefore only go into column 5. That means that no 6 can be in column 5 in either block 2 or block 5 (Locked Candidates Type 1).
The example on the right shows the other variant: In block 8 candidate 6 can only go into column 4, in block 9 only into column 8. Since in both blocks the candidates 6 are confined to rows 7 and 8, in the third block of that chute (block 7) 6 has to be in row 9 (or to put in terms of the definition above: 6 can be safely eliminated from r8c2).
Locked Candidates can be identified easily, when filters are applied for a digit. For an example please see Using Filters in the Users Manual.
Copyright © 2008-12 by Bernhard Hobiger
All material on this page is licensed under the GNU FDLv1.3.

