Last Resort

Table of Contents

Templates

Templates are a single digit pattern method. In an empty sudoku grid exactly 46656 possibilities exist to place all 9 instances of a digit in the grid. Every time an instance of the digit is placed, all combinations that don't contain that cell become invalid, and every time another digit is placed in a cell, all combinations that contain that cell become invalid. If all possible templates have been calculated, the digit can be eliminated from any cell, that is not contained in at least one of the remaining templates, and it can be set in all cells, that are contained in all remaining templates.

From the description it should be clear, that Templates are not meant for human players. They can however be used as indicators: If no Template eliminations are present, no instance of a single digit pattern can possibly be found (e.g.: a very time consuming search for complex fish types is not necessary). The other way round is not necessarily valid.

Forcing Chain

Before you try to dig into Forcing Chains or Nets, please make sure that you have completely understood the Introduction about chains.

Forcing Chain is a generic term for any chain that leads to a contradiction or a verity and thus forces something (any Discontinuous Nice Loop or any AIC is a Forcing Chain by that definition). Chains that don't lead to a contradiction themselves can be combined to a Multiple Forcing Chain. All chains together can either prove a verity or a contradiction, thus leading to a forcing.

In a verity, multiple chains have the same outcome. If one of the premises of the chains has to be true, the result must be true. Examples for premises that can provide a verity:

In a contradiction, all chains start with the same premise, but lead to implications that cannot all be true. Examples for contradictions:

The possibilities of Multiple Forcing Chains are nearly limitless.

If a Forcing Chain or Net is viewed in HoDoKu, the sheer number of links can render the image completely useless. It is therefore possible to show only one chain at a time (see Using the Hint System in the Users Manual).

Sudoku technique: Example for Forcing+Chain+Verity+%28all+chains%29 Sudoku technique: Example for Forcing+Chain+Verity+%28only+chain+1%29 Sudoku technique: Example for Forcing+Chain+Verity+%28only+chain+2%29 Sudoku technique: Example for Forcing+Chain+Verity+%28only+chain+3%29

The example shows a rather simple Forcing Chain Verity, that proves that r1c7 has to be 4 (the first image shows all links at once, the other three images show the three chains).

Forcing Chain Verity => r1c7=4

Meaning: For every possible placement of digit 1 in row 4 it can be proved that r1c7 is 4. r1c7 must therefore be 4.

For every Forcing Chain Verity a complementary Forcing Chain Contradiction exists. The contradiction for the example above:

Forcing Chain Contradiction in r4 => r1c7=4

Meaning: If r1c7 is not 4, row 4 doesn't contain digit 1. Since this is not possible, the premise must be wrong, 4 can be placed in r1c7.

Forcing Net

A Forcing Net is build on the same principle than a Forcing Chain, but as net and not as chain (see Chains versus Nets). They are a real "Last Ressort" method and can be found manually only by very experienced players (the images below speak for themselves).

Notation: The branches of the net are put in parenthesis. There outcome is used later on in the net.

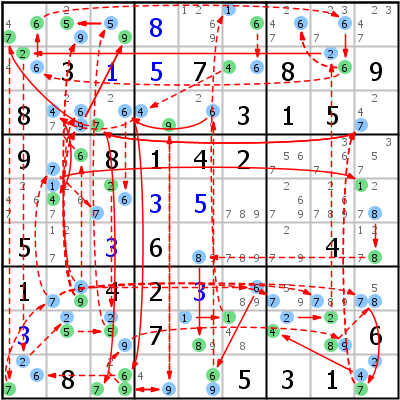
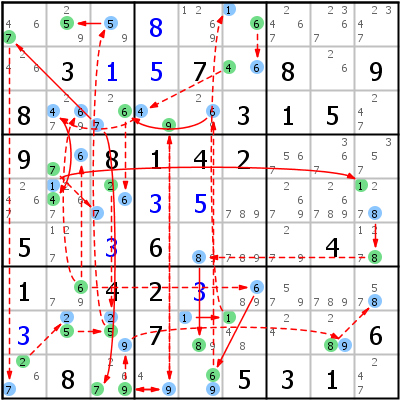
Sudoku technique: Example for Forcing+Net+Verity+%28all+chains%29 Sudoku technique: Example for Forcing+Net+Verity+%28only+net+1%29 Sudoku technique: Example for Forcing+Net+Verity+%28only+net+2%29 Sudoku technique: Example for Forcing+Net+Verity+%28only+net+3%29

The example is a verity that proves that r1c2 has to be 5.

Forcing Net Verity => r1c2=5

Meaning: Cell r7c2 has three possibilities left: 6, 7, and 9. No matter which digit will finally be placed in r7c2, r1c2 is always 5.

Let's study the last (and simplest) net. If we ignore the parenthesis, we can follow the chain nicely: If r7c2 is 9, r3c2 cannot be 9. Here we are stuck. We cannot continue, because 9 in r3c2 and r1c3 are only weakly linked (additional 9 in r1c2). Fortunately, 9 in r1c2 cannot be true as well if r7c2 is 9 (the branch of the net), thus turning the weak link into a strong link.

The branches in the other nets cannot be so easily explained. Just try to decipher them yourself.

Kraken Fish

A Kraken Fish is the combination of a fish with one or more chains. It usually uses Finned Fishes, that don't provide eliminations, because the possible eliminations cannot see all fins (see Fish General).

Kraken Fish Type 1

In a finned fish a possible elimination becomes an actual elimination, if it can see all the fins. More often than not, this is not the case, and we get a useless finned fish without eliminations. A Kraken Fish can squeaze an elimination out of such a fish by using chains.

The premise for a finned fish was: If all fins are false, all possible eliminations become valid. But if a fin is true, the fish is destroyed and the placement eliminates all candidates of the fish digit in the peers of the fin.

In a Kraken Fish, that principle is simply enhanced: If we can prove that a possible elimination must be false for all possible fins, we can eliminate that candidate. The prove uses chains that start with a weak link in every fin and end in a weak link in the possible elimination.

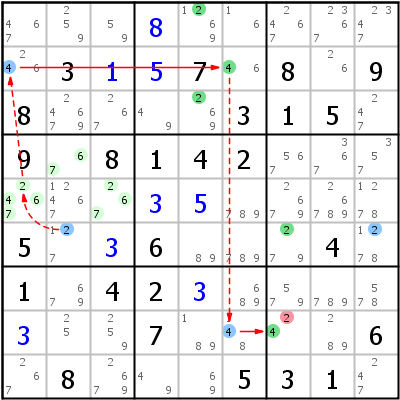
Sudoku technique: Example for Kraken+Fish+Type+1+%28Chain+1%29 Sudoku technique: Example for Kraken+Fish+Type+1+%28Chain+2%29

The example is from the same sudoku state. in which the Forcing Net from the example above was necessary. The basis is a Finned Franken X-Wing: 2 r6b2 c57 fr6c2 fr6c9. Possible eliminations are r158c7 (none of those see both fins).

The image on the left shows the first chain connecting fin r6c2 to r8c7: r6c2 -2- ALS:r4c2,r5c13 -4- r2c1 =4= r2c6 -4- r8c6 =4= r8c7. The image on the right shows the second chain for the second fin (r6c9): r6c9 -2- ALS:r13479c9 -8- ALS:r8c238 -2- r8c7.

Meaning:

This is a typical verity.

Kraken Fish Type 2

Type 2 gets slightly more complicated than type 1. Let us review what a fish is all about: It guarantees that exactly one base candidate is true in all cover sets.

If we can build chains, starting with a weak link each, from each base candidate in one of the cover sets plus from each fin (if present), that lead to the same conclusion, we have a Forcing Chain verity.

Sudoku technique: Example for Kraken+Fish+Type+2+%28Fish+only%29 Sudoku technique: Example for Kraken+Fish+Type+2+%28Chain+1%29 Sudoku technique: Example for Kraken+Fish+Type+2+%28Chain+2%29 Sudoku technique: Example for Kraken+Fish+Type+2+%28Chain+3%29

The example shows a Kraken Fish based on a Sashimi X-Wing: 4 r15 c12 fr1c7 fr1c9. What is good for us is that cover set column 2 has only one base candidate (r5c2). The other 4 in that column (r3c2) is a cover candidate and doesn't interest us now. We can build the following chains:

Together they prove that r5c9 cannot be 7.

Brute Force

Brute Force is not really a technique: Place a digit in a cell and look, whether you get a solution or not. If that technique is enabled, every sudoku can be solved.

Copyright © 2008-12 by Bernhard Hobiger
All material on this page is licensed under the GNU FDLv1.3.